Exercise 6.3
1. State which pairs of triangles in the figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
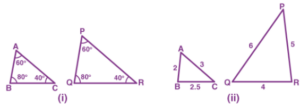
solution:
click here to watch on youtube
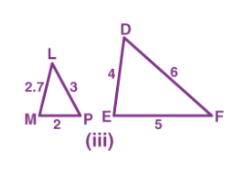
solution:
click here to watch on youtube
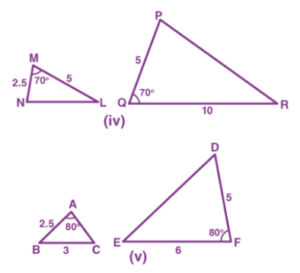
solution:
click here to watch on youtube
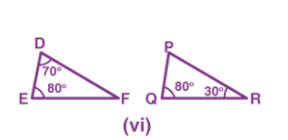
solution:
click here to watch on youtube
2. In figure 6.35, ΔODC ~ ΔOBA, ∠ BOC = 125° and ∠ CDO = 70°. Find ∠ DOC, ∠ DCO and ∠ OAB.

solution:
click here to watch on youtube
3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that AO/OC = OB/OD

solution:
click here to watch on youtube
4. In the fig.6.36, QR/QS = QT/PR and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

solution:
click here to watch on youtube
5. S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ~ ΔRTS.
solution:
click here to watch on youtube
6. In the figure, if ΔABE ≅ ΔACD, show that ΔADE ~ ΔABC.

solution:
click here to watch on youtube
7. In the figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
solution:
click here to watch on youtube
8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ~ ΔCFB.
solution:
click here to watch on youtube
9. In the figure, ABC and AMP are two right triangles, right angled at B and M, respectively, prove that:

(i) ΔABC ~ ΔAMP
(ii) CA/PA = BC/MP
solution:
click here to watch on youtube
10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC ~ ΔFEG, Show that:
(i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
solution:
click here to watch on youtube
11. In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ~ ΔECF.

solution:
click here to watch on youtube
12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR (see Fig 6.41). Show that ΔABC ~ ΔPQR.

solution:
click here to watch on youtube
13. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD
solution:
click here to watch on youtube
14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
solution:
click here to watch on youtube
15. A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
solution:
click here to watch on youtube
16. If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR prove that AB/PQ = AD/PM.
solution:
click here to watch on youtube